Authors: Kai Yang (Institute for Astronomy, University of Hawaii at Manoa)

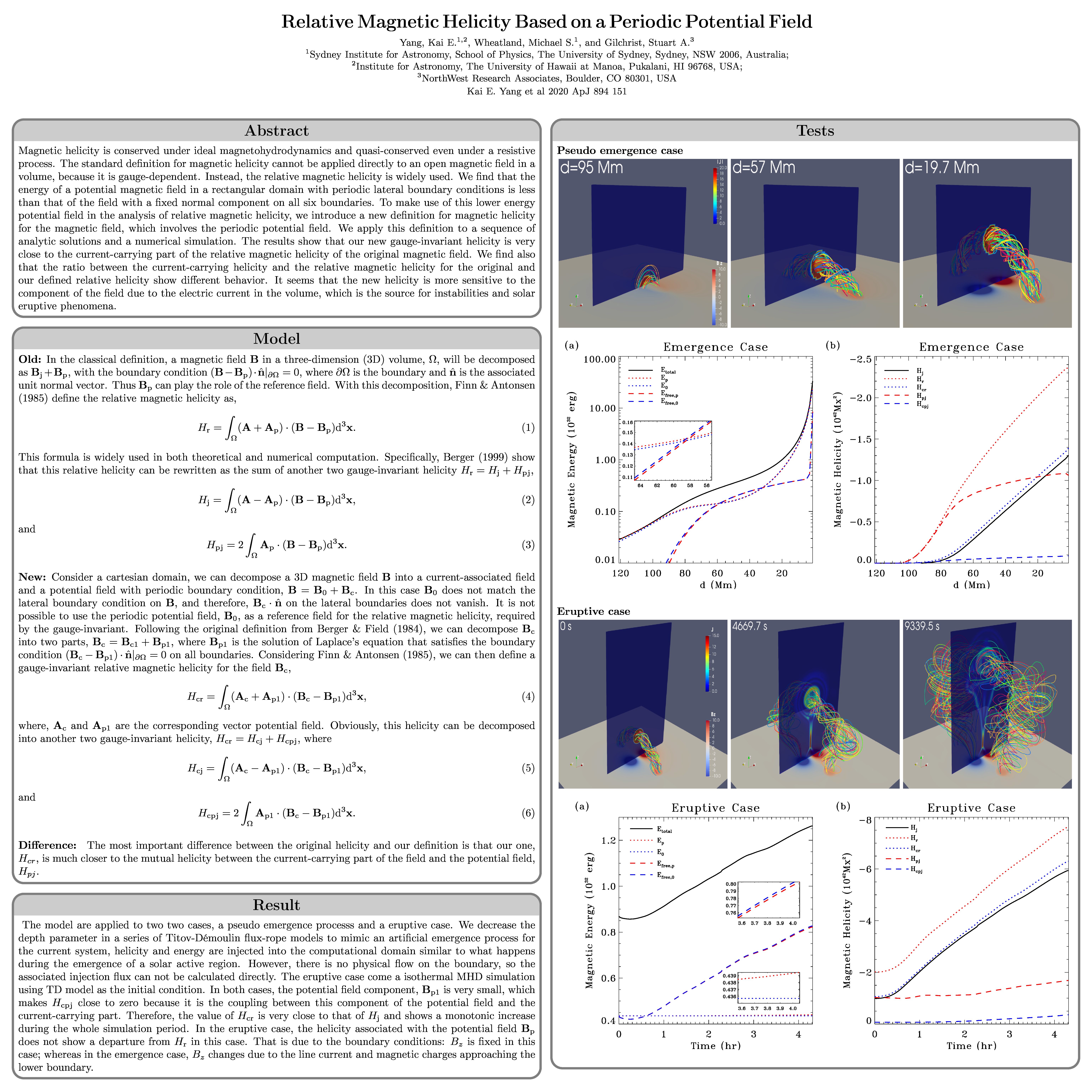
Magnetic helicity is conserved under ideal magnetohydrodynamics and quasi-conserved even under a resistive process. However, the standard definition for magnetic helicity cannot be applied directly to an open magnetic field in a volume because it is gauge-dependent. Instead, the relative magnetic helicity is widely used. We find that the energy of a potential magnetic field in a rectangular domain with periodic lateral boundary conditions is less than that of the field with a fixed normal component on all six boundaries. To use this lower energy potential field in the analysis of relative magnetic helicity, we introduce a new definition for magnetic helicity for the magnetic field, which involves the periodic potential field. We apply this definition to a sequence of analytic solutions and a numerical simulation. The results show that our new gauge-invariant helicity is very close to the current-carrying part of the relative magnetic helicity of the original magnetic field. We also find that the ratio between the current-carrying helicity and the relative magnetic helicity for the original and our defined relative helicity show different behavior. It seems that the new helicity is more sensitive to the component of the field due to the electric current in the volume, which is the source of instabilities and solar eruptive phenomena.